アラン分散

アラン分散（Allan variance）は、時計、発振器、アンプにおける周波数安定度を表す指標である。名前はDavid W. Allanに由来し、数学的には${\displaystyle \sigma _{y}^{2}(\tau )}$ と表される。 アラン偏差（Allan deviation）は、アラン分散の平方根である${\displaystyle \sigma _{y}(\tau )}$ である。

アラン分散は統計的な安定度を推定するためのものであり、周波数ドリフトなどの系統的な誤差を推定するものではない。また、アラン分散には、修正アラン分散をはじめとするいくつかの派生形がある。

背景

水晶発振器や原子時計の安定性が調べられていた頃、位相ノイズにはホワイトノイズのみならず、フリッカー周波数ノイズも存在しているとわかった。これらのノイズの形は、推定値が収束しないため、標準偏差などの伝統的な統計ツールでは扱いが難しい。安定性を分析する初期の取り組みは、理論的な分析と実用的な測定の両方から行われた。

この問題を解決するため、David AllanはM-サンプル分散を導入し、間接的にアラン分散（2-サンプル分散）を導入した。アラン分散では、全ての種類のノイズを見分けることはできないが、有意義な情報が得られる。IEEEはのちに、M-サンプル分散よりもアラン分散（2-サンプル分散）の方が望ましいとみなした。

定義

振動と位相ノイズ

振動は以下の式で表される。

${\displaystyle V(t)=V_{0}\sin(\Phi (t)).}$

位相は以下のように表される。

${\displaystyle \Phi (t)=\omega _{\text{n}}t \varphi (t)=2\pi \nu _{\text{n}}t \varphi (t).}$

${\displaystyle \nu _{\text{n}}}$は基準となる周波数を表し、${\displaystyle \varphi (t)}$は位相ノイズを表す。

周波数

瞬間的な周波数は、位相の時間微分で表される。

${\displaystyle \nu (t)={\frac {1}{2\pi }}{\frac {d\Phi (t)}{dt}}.}$

規格化された周波数偏差

瞬間的な周波数の、基準となる周波数からの偏差を規格化して、以下の量を定義する。

${\displaystyle y(t)={\frac {\nu (t)-\nu _{\text{n}}}{\nu _{\text{n}}}}={\frac {\nu (t)}{\nu _{\text{n}}}}-1.}$

規格化された周波数偏差の時間平均

規格化された周波数偏差の時間平均は以下のように定義される。

${\displaystyle {\bar {y}}(t,\tau )={\frac {1}{\tau }}\int _{0}^{\tau }y(t t_{v})\,dt_{v},}$

ここでτは平均化時間を表す。

アラン分散

n番目の周波数偏差を以下のように表すとする。

${\displaystyle {\bar {y}}_{n}={\bar {y}}(n\tau ,\tau )}$

アラン分散は以下のように定義される。

${\displaystyle \sigma _{y}^{2}(\tau )={\frac {1}{2}}\left\langle \left({\bar {y}}_{n 1}-{\bar {y}}_{n}\right)^{2}\right\rangle }$

ただし、${\displaystyle \langle \dotsm \rangle }$は期待値を表す。

アラン偏差

標準偏差と分散の関係と同様に、アラン偏差はアラン分散の平方根として定義される。

${\displaystyle \sigma _{y}(\tau )={\sqrt {\sigma _{y}^{2}(\tau )}}.}$

べき乗ノイズ

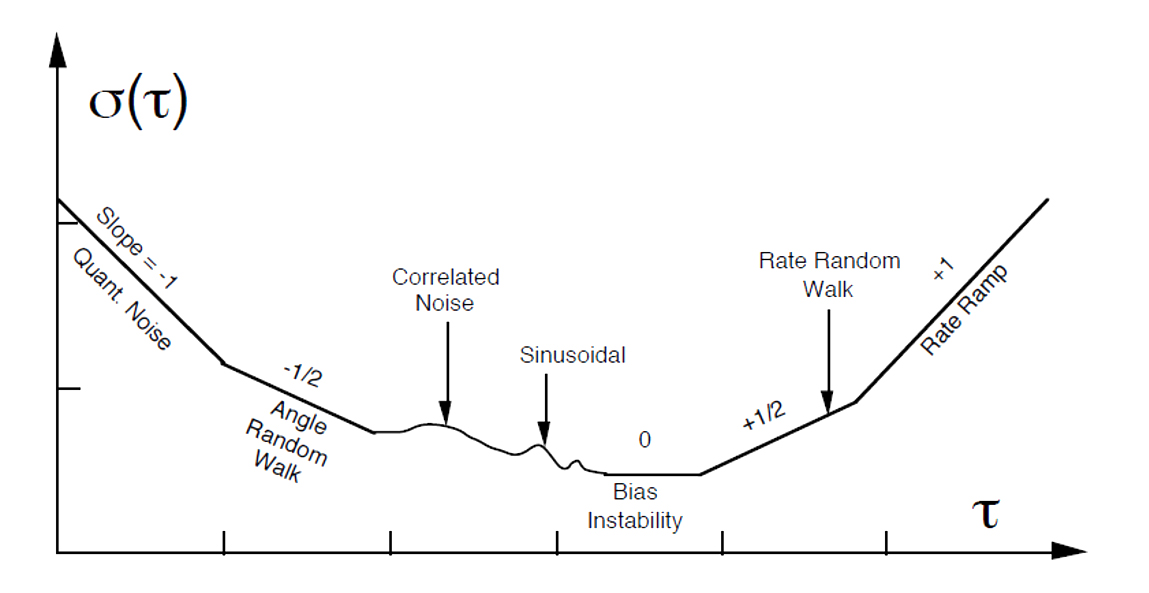
アラン分散は、さまざまなべき乗ノイズを見分けることができる。

アラン分散は、白色位相ノイズとフリッカー位相ノイズを見分けることができない。一方で、修正アラン分散ではこれらを見分けることができる。

線形応答

アラン分散は、位相や周波数に乗るノイズを見分けるためのものである。一方で、位相や周波数の線形な変化に対して依存性を示すことがある。

上の表より、アラン分散は、位相や周波数に定数のオフセットがついても変化しないが、周波数が線形に変化すると影響を受ける。

関連項目

• 分散
• 計量学

出典